近日，我院光电子智能器件与系统团队通过理论研究证明，不同于时间反演对称，时间空间联合反演对称（PT）对手性时域耦合模理论的耦合系数与背景散射矩阵有新的限制。相关研究成果以“Temporal coupled-mode theory for PT-symmetric chiral metasurfaces”为题发表在《Optics Letters》 (Optics Letters, 48, 5503, 2023) 。

对称性在物理学中占有非常重要的地位，基于波函数的统计诠释，Wigner 认为对称性变换只能是幺正变换或者反幺正变换，其中幺正对称性变换存在对应的守恒量，反幺正变换则不然。最近几年，非厄米物理系统（特别是PT对称的非厄米哈密顿量，PT为反幺正算符，P为空间反演算符，T为时间反演算符）得到科研人员的广泛关注，研究人员发现许多新的物理效应，例如异常点等。时域耦合模理论（TCMT）是研究光学系统，例如光子晶体平板、纳米天线和腔波导耦合系统，非常重要的理论工具。以前人们对TCMT的对称性考虑主要是基于能量守恒、时间反演和Lorentz互易。时间反演对称和互易意味着该系统没有增益和损耗，从而耦合系数与背景散射矩阵有很强的限制，而弱的增益或损耗可以作为一阶微扰考虑进TCMT。

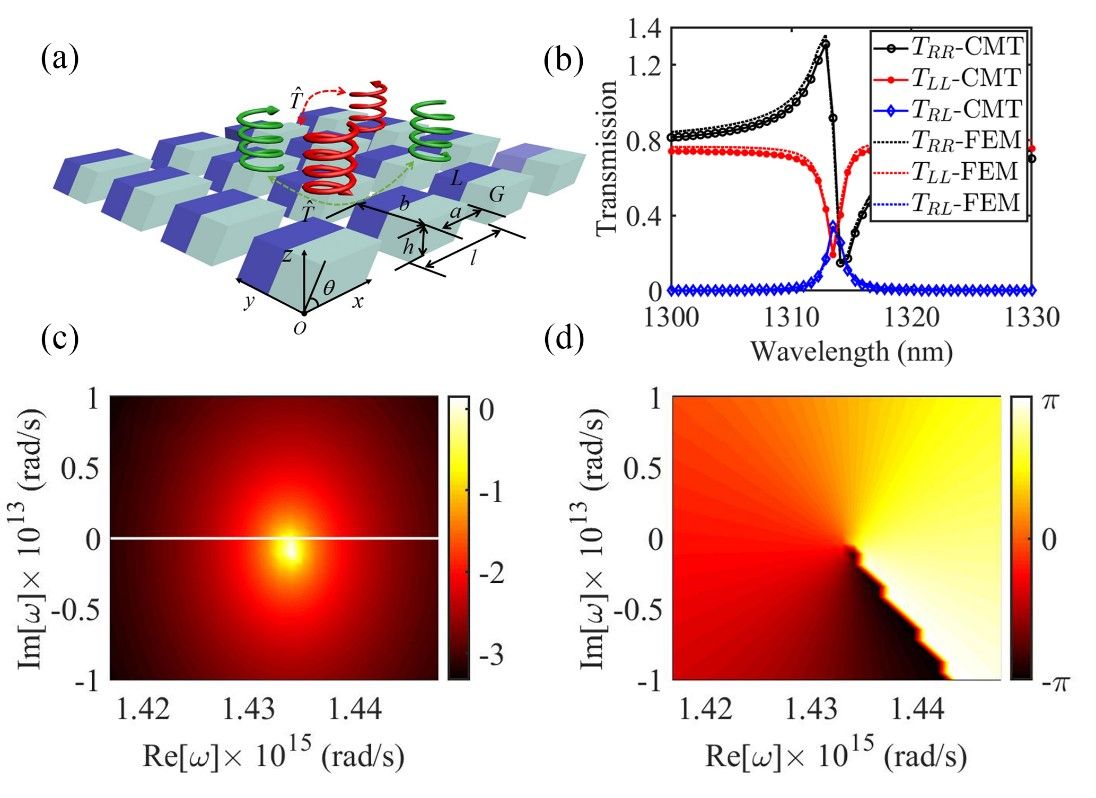
图 (a) PT对称手性超表面结构。(b) 非厄米参数为0.05时手性时域耦合模理论与有限元方法计算的透射谱。(c) 复平面交叉透射系数的振幅。(d) 复平面交叉透射系数的相位。

该团队利用手性TCMT研究PT对称超表面手性相互作用的过程中，发现单独的时间反演对称考虑是不足以描述PT对称系统的，PT对称算符对耦合系数与背景散射矩阵给出新的约束关系。为验证该关系，团队设计一个PT对称超表面，如图（a）所示。在研究波长范围内，超表面能激发手性连续谱中的束缚态（BICs），首先利用准模理论和格林函数计算出时域耦合模理论中的耦合系数，然后利用该关系导出背景散射系数，从而计算整个散射矩阵，理论结果与有限元数值计算结果高度一致，如图（b）所示。手性TCMT可以直接解析延拓到复频率平面，其复平面的交叉圆透射系数的振幅如图（c）所示，清楚地显示共振极点的位置。交叉圆透射系数的相位如图（d）所示，可以看出共振极点是复频率空间的拓扑缺陷，即相奇异，其拓扑荷为-1。

该工作为研究非厄米超表面增强的手性共振作用提供了理论基础。合肥工业大学为论文第一单位，hbs红宝石平台陈小林老师为论文第一作者，高伟清教授为论文通讯作者。该工作得到了国家重点研发计划、国家自然科学基金和合肥工业大学中央高校业务费等项目的支持。

文章链接：https://doi.org/10.1364/OL.505451

 （陈小林/图文  高伟清/审核）